Genetic Sequences
This is a compendium of the article and software library I wrote about parsing genomic sequences stored in a textual format (ASCII). The results of this effort is the ISO C++ library libseq, freely available and open source.
Scientific publications are really coincise, and this page will guide you through the thought process I used to accelerate textual parsing with Intel's SIMD SSE instructions. I hope you get a better idea about SIMD instructions, and in this page I will use Intel's intrinsics, the C equivalent of assembly opcodes, as I think it is clearer, and because I've developed it using intrinsics and not assembly.
Enjoy.
Abstract
Sequencing technologies are literally bringing new challenges in the genomics field. What once were room-sized hardware, they shrank to the size of a small refrigerator. Now they literally are in the palm of our hands.
This incremental change brought challenges. The first sequencers, hardware that translates DNA sequences into a textual representation, were slow. However, this progressively improved over time, and now we have sequencers whose output is within the tens of gigabyte range. For instance, Illumina NovaSeq 6000 outputs up to 6 Terabases (Tb), and Nanopore’s PromethION reaches 7.3 Tb, with read lengths ranging from thousands to hundred thousands of base pairs.
We're all familiar with DNA, constituted by adenosine ("A"), cytosine ("C"), thymine ("T"), and guanine ("G"), these are called bases, and are translated into ASCII characters. Since we're dealing with billions and billions of bases, parsing these large files is an important step for the DNA analysis process. Here, I will show how I improved parsing using Intel's intrinsics, and this approach is easily portable to NEON instructions found on ARM processors.
Needless to say, the whole problem relies in converting DNA sequences into a numeric representation, before proceeding to futher analyses. This is the problem that we're interested in.
Representing a k-mer
The first thing you'll learn about this whole process is that analysis softwares do not use the whole DNA sequences. In fact, the output of sequencers is not a sequence of bases. For technical reasons, DNA is multiplied and cut into pieces of various lengths, called reads. Since we do not know where the DNA was cut to be read by the sequencer, using whole reads is pointless, moreover, sequencers can output a certain number of bases per read. We need to abandon the idea that sequencers give us a real DNA sequence: the correct genome is then the output of various programs (error corrections, assembly, ...).
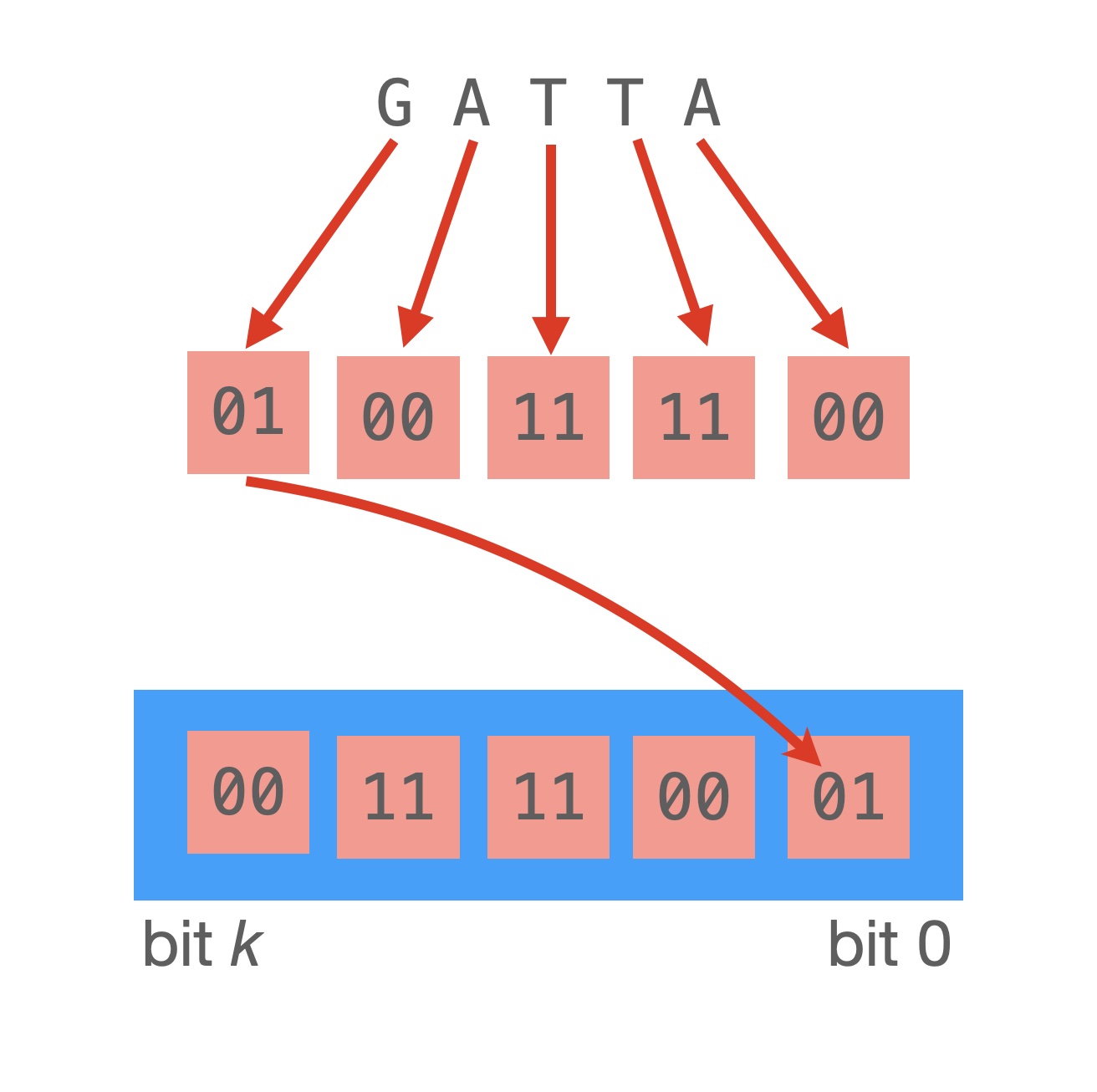
The most common way to reconstruct a sequence is by using k-mers, in other words, substrings of length k. As genomic files use four letters, we just need two bits per letter, as you can see in the picture. Here we selected A = 0 = 00b, T = 3 = 11b, C = 1 = 01b, G = 2 = 10b for convenience: what is also important in DNA analyses is not only the forward k-mer, but also its reverse complement, the reversed string with complementary nucleotides. So where there is A, we substitute with T; and for C we substitute G (and viceversa).
An Example of k-mers
ATAC -> 00 11 00 01 (forward) GTAT -> 10 11 00 11 (reverse complement) GATTACA -> 10 00 11 11 00 01 00 (forward) TGTAATC -> 11 10 11 00 00 11 01 (reverse complement)
Curiously Recurring
Our objective is to read these files as fast as possible, converting all the reads to a sequence of bits, or in other terms, to an integer.
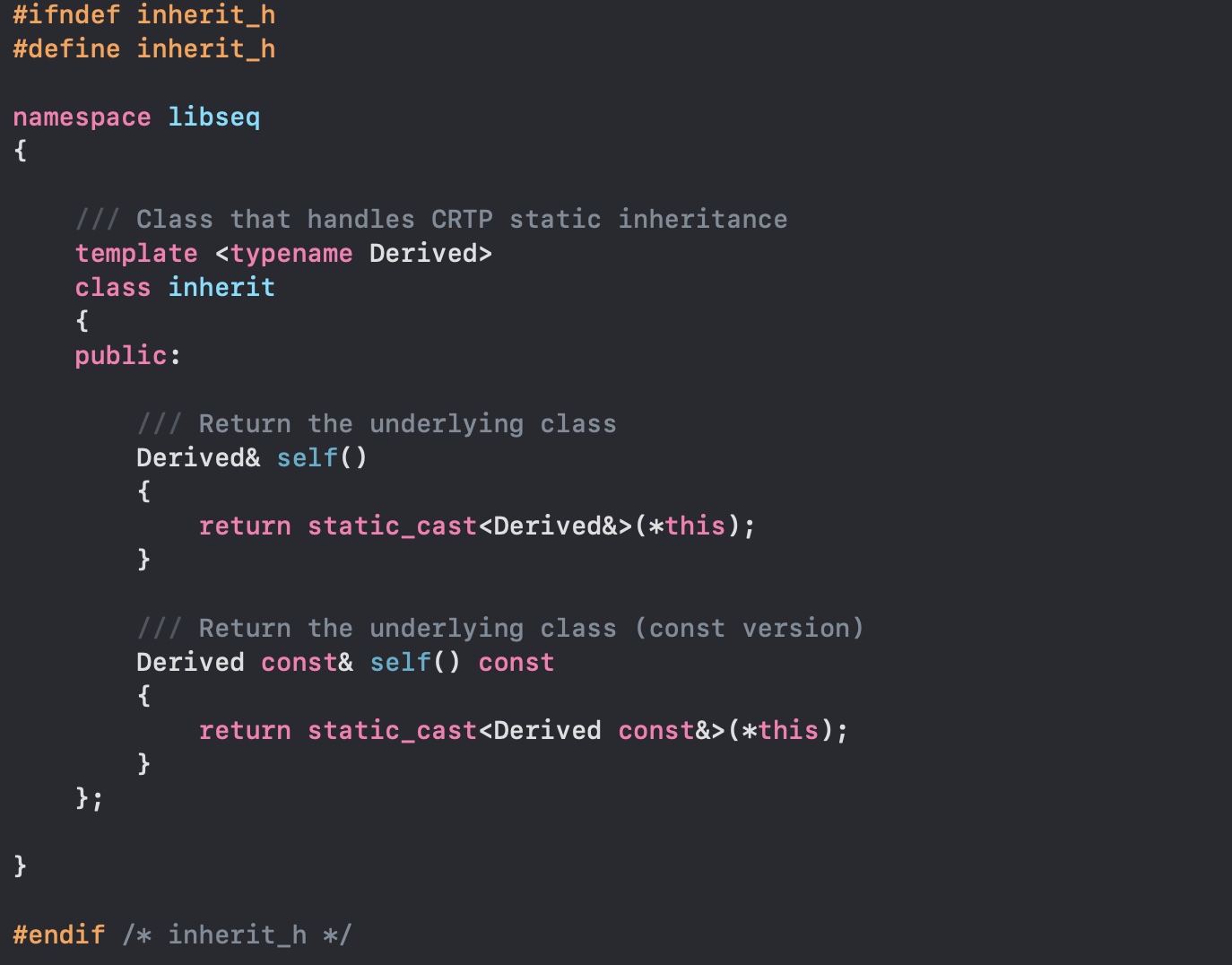
But DNA files can have at least three textual formats: how can we avoid paying the price for inheritance and being able to switch classes? C++ have you covered, we will use the Curiously Recurring Template Pattern. You know we can have templated classes, "generics" if you need, and you can inherit from a class... but nothing prohibits to inherit from a template with yourself as parameter. This way it's a static polymorphism that won't pay any overhead.
Iterators
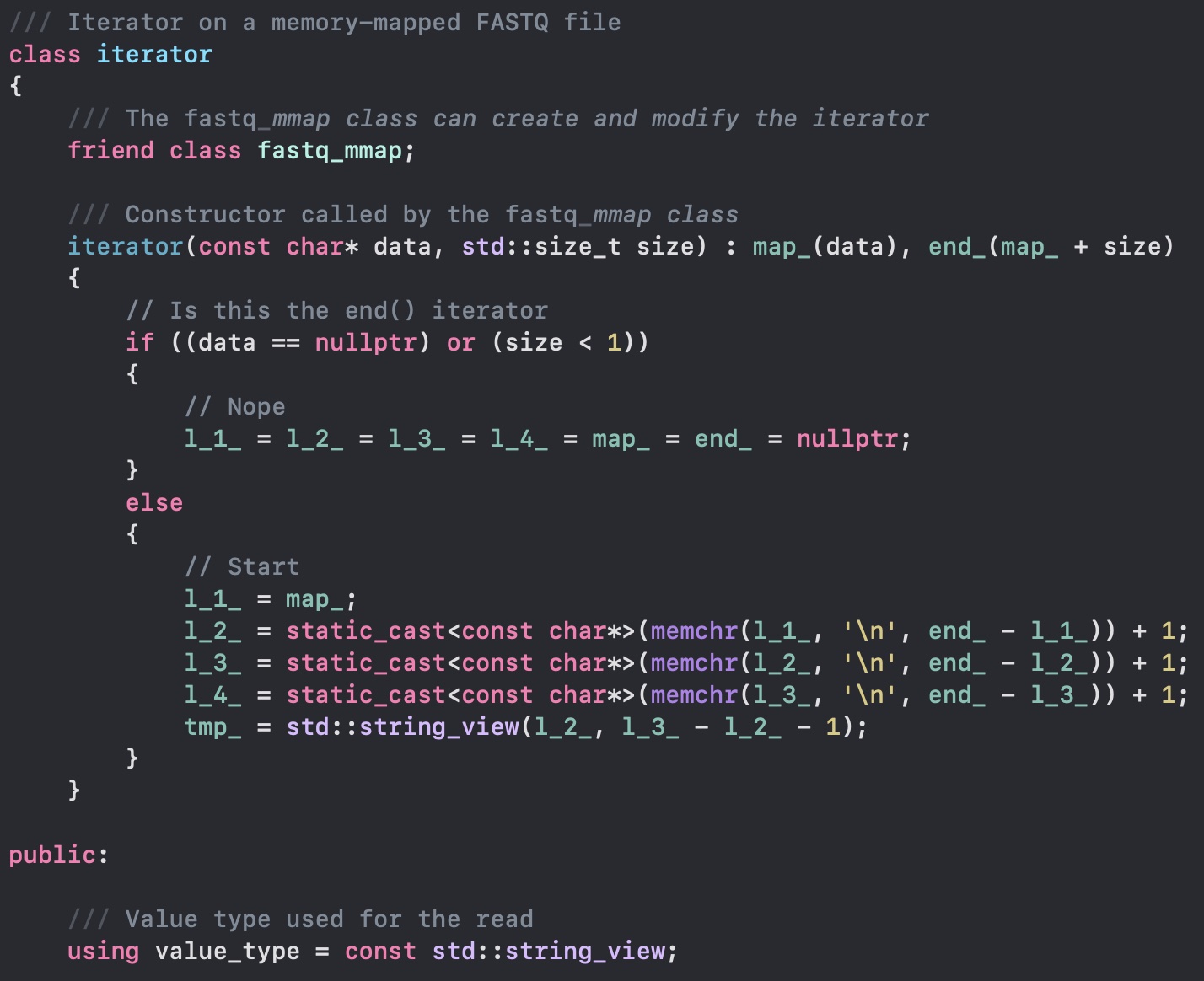
Now we want to read all the DNA sequences from a file. Since we have a memory mapped file, we can access the contents of the file as if it were in memory. The workload will be handled by the operating system, and this is really fast. We have to decide what basic data structure to use for parsing the file. A string would be too slow: it allocates memory... yes, it might have small-string optimization, but no string is better than a string, especially when you are dealing with billions and billions of them. When strings fail, of course we use string_view: it does not hold any memory, aside from the memory address where the string is located. This is perfect, as our file is already in memory! To complete the quest, we avoid also all C++ string search and rely on the always optimized memchr functions.
Accelerating Parsing
Basically parsing has as input a string (string_view), and outputs an integer. Can we accelerate this via hardware?
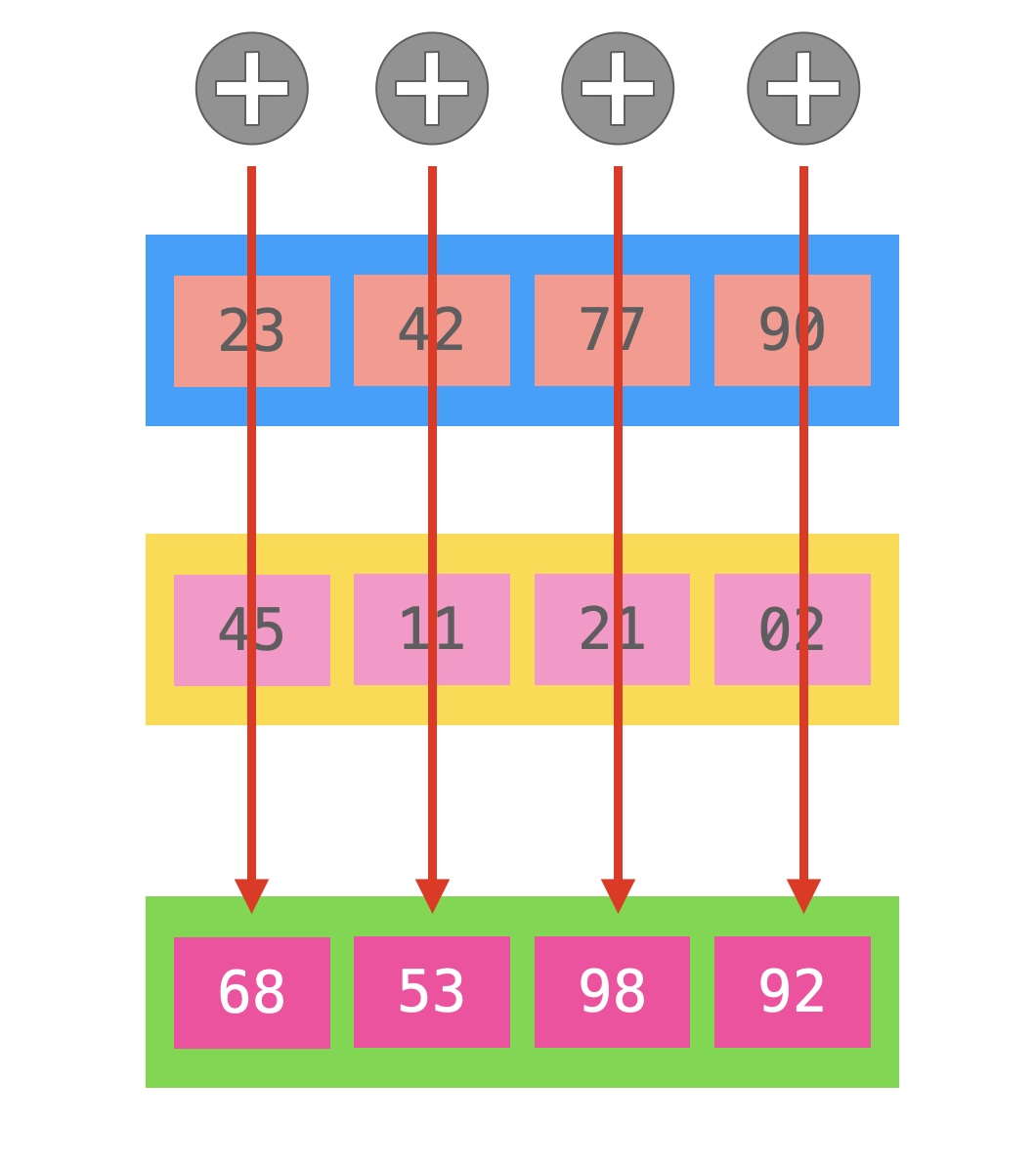
Back in the 1960s ILLIAC IV introduced Single Instruction Multiple Data opcodes (or SIMD): a way of processing more data with the very same operation. In the picture we are adding four integers in a single instruction. Intel started providing SIMD instructions in 1998 with the 64-bit MMX (Multimedia Extension), modern processors have SSE (128 bits), AVX and AVX-2 (256 bits), and on Xeons we have AVX-512 (512 bits).
With these instructions we can process a large number of bytes, interpreting them as we want, for instance, 128 bits can be seen as two 64-bits integers or floats, four 32-bits and so on. On a particular note, all SIMD instructions cannot use normal registers. These instructions must use special purpose registers called MM0, MM1, ... (MMX); XMM0, XMM1, ... (SSE); YMM0, YMM1, ... (AVX and AVX-2); and ZMM0, ZMM1, ... (AVX-512).
A Different Mindset
Now the parsing is quite straightforward: just load the data in memory, convert it to an integer, and with SIMD we can process many nucleotides in one instruction, 16 in a single clock cycle (more or less). The problem is that I would need to process these bytes in a SIMD register and then rearranging them in the integer, as you have seen before. So that ATAC will be in memory 00=A 11=T 00=A 01=C. Moving around bits is expensive and defeats the purpose of SIMD to process everything in a cycle. But then, it occurred to me...
Why would I ever need to rearrange the bits?
As long as I can process everything fast, where a nucleotide is remains an immaterial problem. So let's move to loading all possible bytes in memory and then converting to bits. How many registers we will use? Here we will use SSE for maximum compatibility, it sports 128-bits registers, so we can store 64 nucleotides in a single integer. We will need therefore 4 SIMD registers to load all these 64 bytes in memory.
From ASCII to Bits
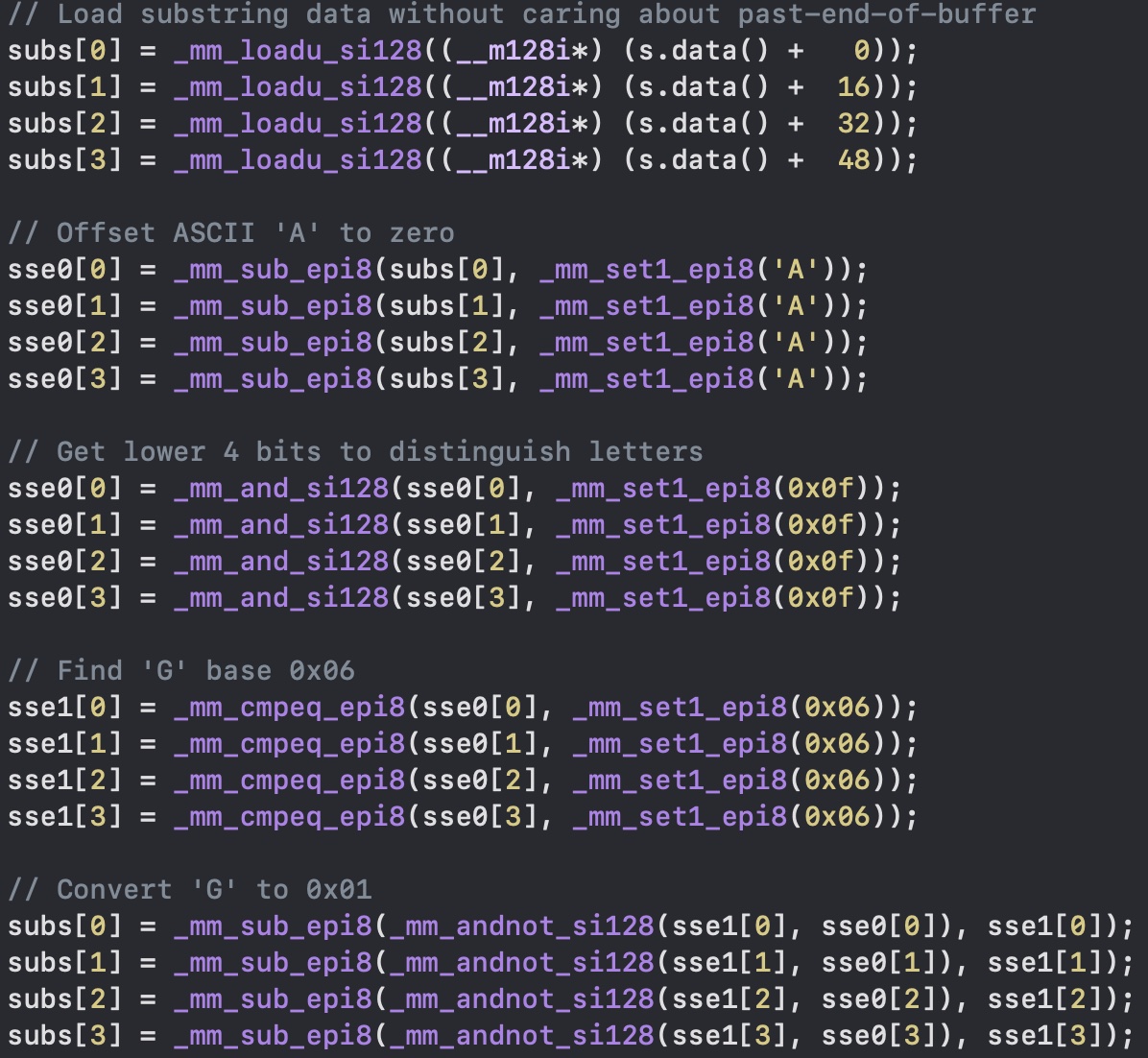
First let's take a look at the ASCII table. The "A" is 65, in bits is 0100 0001, "C" is 0100 0011, "G" is 0100 0111, and "T" is 0101 0100. Take a good look at it, and you'll see that the last two bits are almost perfectly unique for each nucleotide... except for "G".
So the first thing we do is to load all 64 bytes with _mm_loadu_si128 (unaligned load), and subtract "A" from each one with _mm_sub_epi8. Then to distinguish each nucleotide we need to mask the last 4 bits with _mm_and_si128 using a value constituted by all 1s in the least significant bits (_mm_set1_epi8). Now we obtain the following: "A" = 0000 0000, "C" = 0000 0010, "G" = 0000 0110, and "T" = 0000 0011.
As the last step we have to take care of "G". This is easily done with _mm_cmpeq_epi8 that finds all the "G"s in the register, and then replace them with _mm_andnot_si128 and _mm_sub_epi8.
Moving in Place
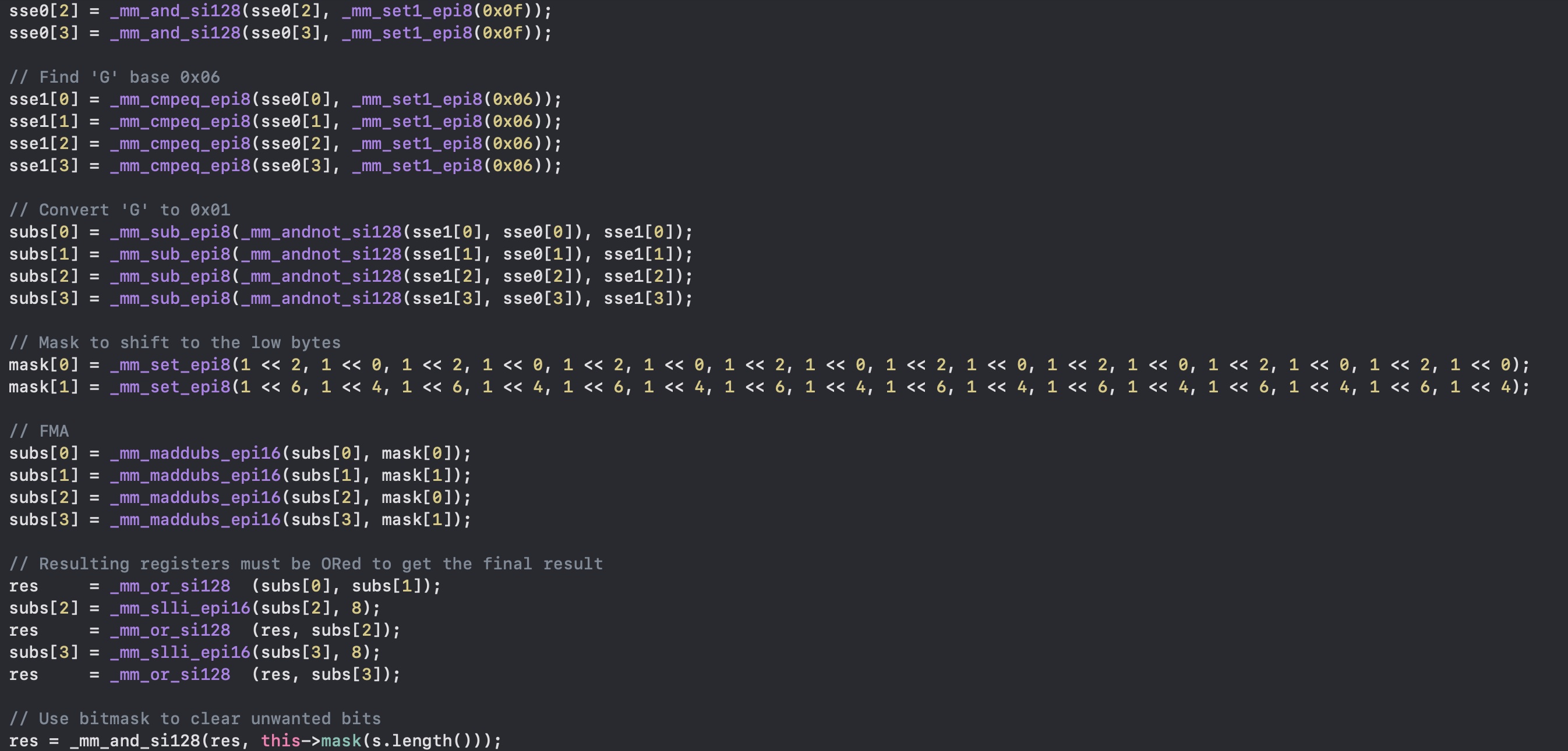
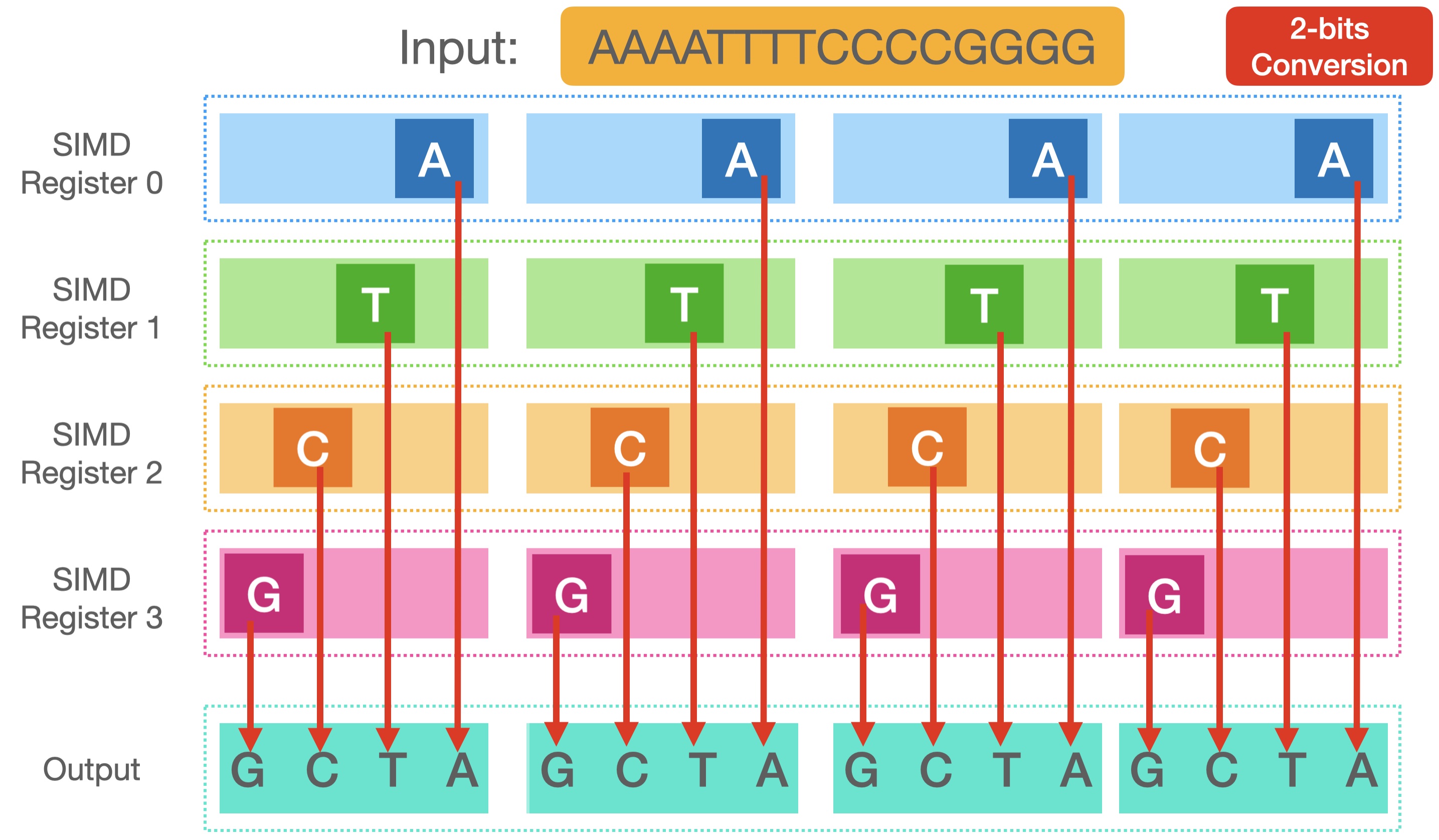
Now that we loaded four registers with the bytes, and converted them to 2-bits, we have one last problem: they are all in the same place. Each register contains 2 bits placed in every byte of it. However, we don't want them overlapping, we need a unique location for each nucleotide, just as you see in the picture.
Fused Multiply-Add
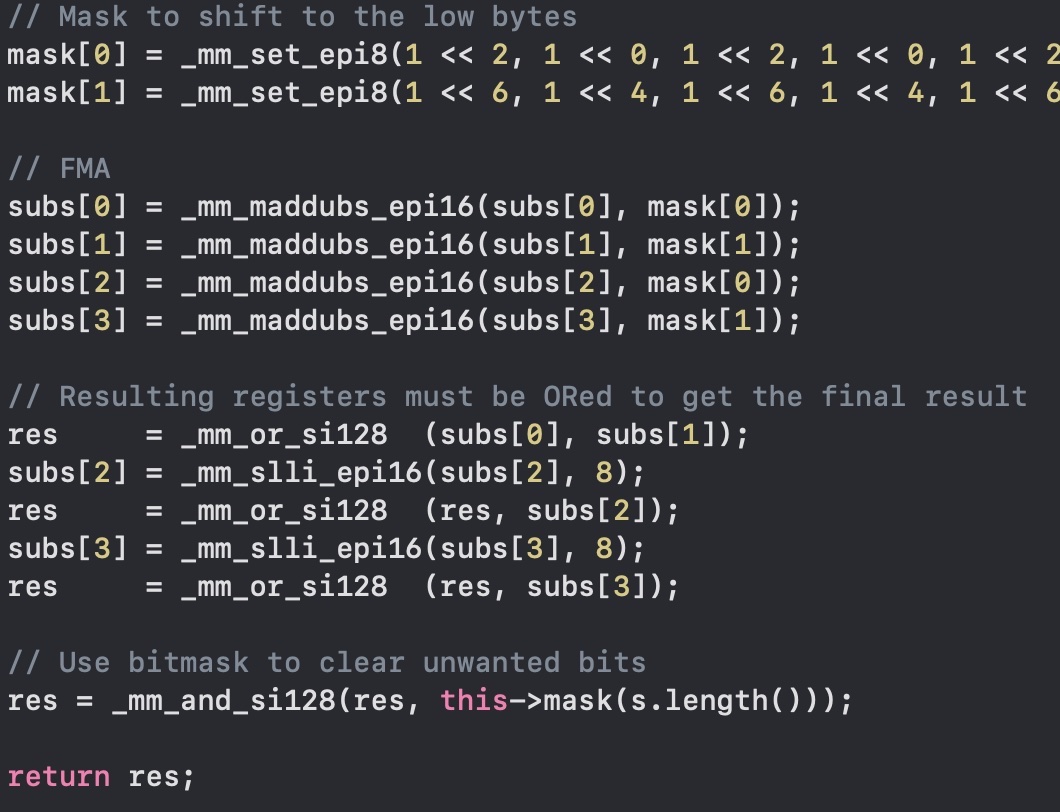
I don't have a fancy processor (I had an old Intel MacBook Pro, now an M2 Pro) that has a real FMA hardware, but we can get close. As you know, moving bits around here is
Finally we can OR the results with _mm_or_si128 and shift left the bytes (not bits) with _mm_slli_epi16.
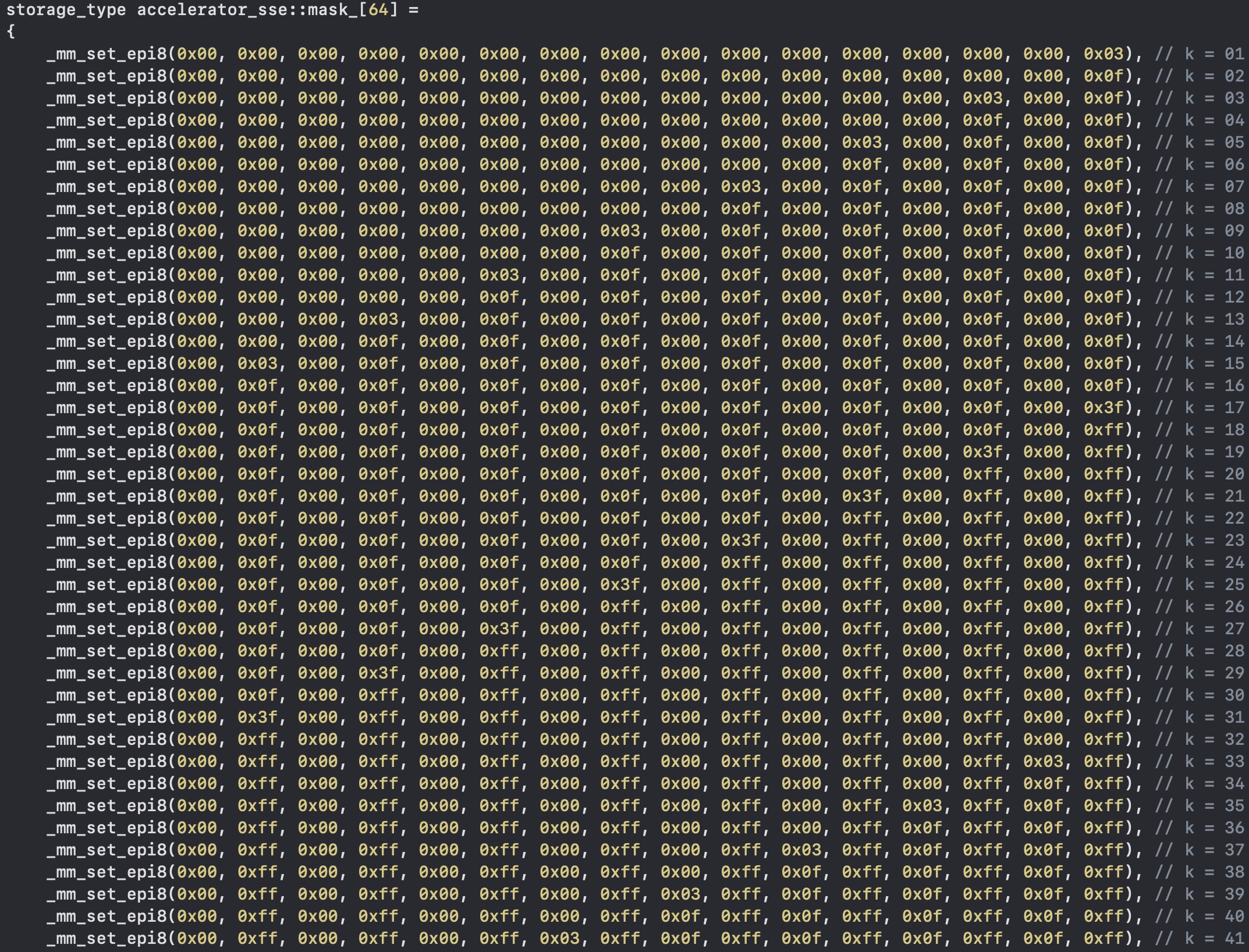
Bitmasks
Once we have all the bits in the right place, we must remember the first lines of code: we're loading 4 128-bits in memory regardless of the substring length. This means that we have some garbage inside our final output register.
Precomputing the bitmasks that leave only the first k nucleotide in place is quite easy, and with _mm_and_si128 we can clear the spurious bits. Even processing more than k bytes at a time, I can assure you this is really, really fast.
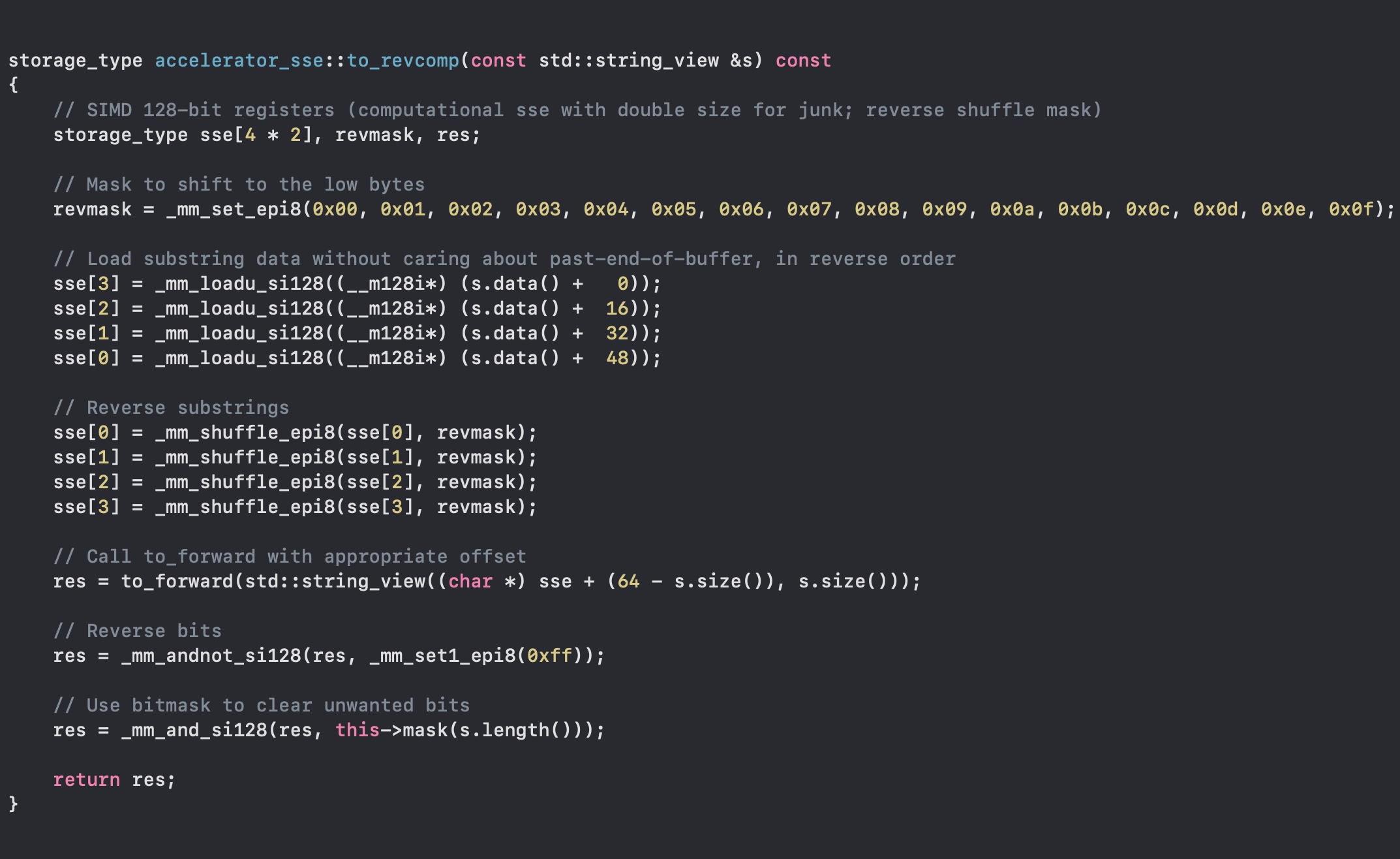
Reverse Complement
How now can we compute the reverse complement? Remember that the reverse complement is simply the string reversed, and then substituting the complementary nucleotides (A-T, C-G).Well, this is quite easy, as a matter of fact. Here I can just load the string, reverse the bytes with _mm_shuffle_epi8, and call the forward routine! What about the complement? Easy. We chose A-T and C-G to be the not-inverse of each other, so an _mm_andnot_si128 is enough (and let's clear the garbage again).
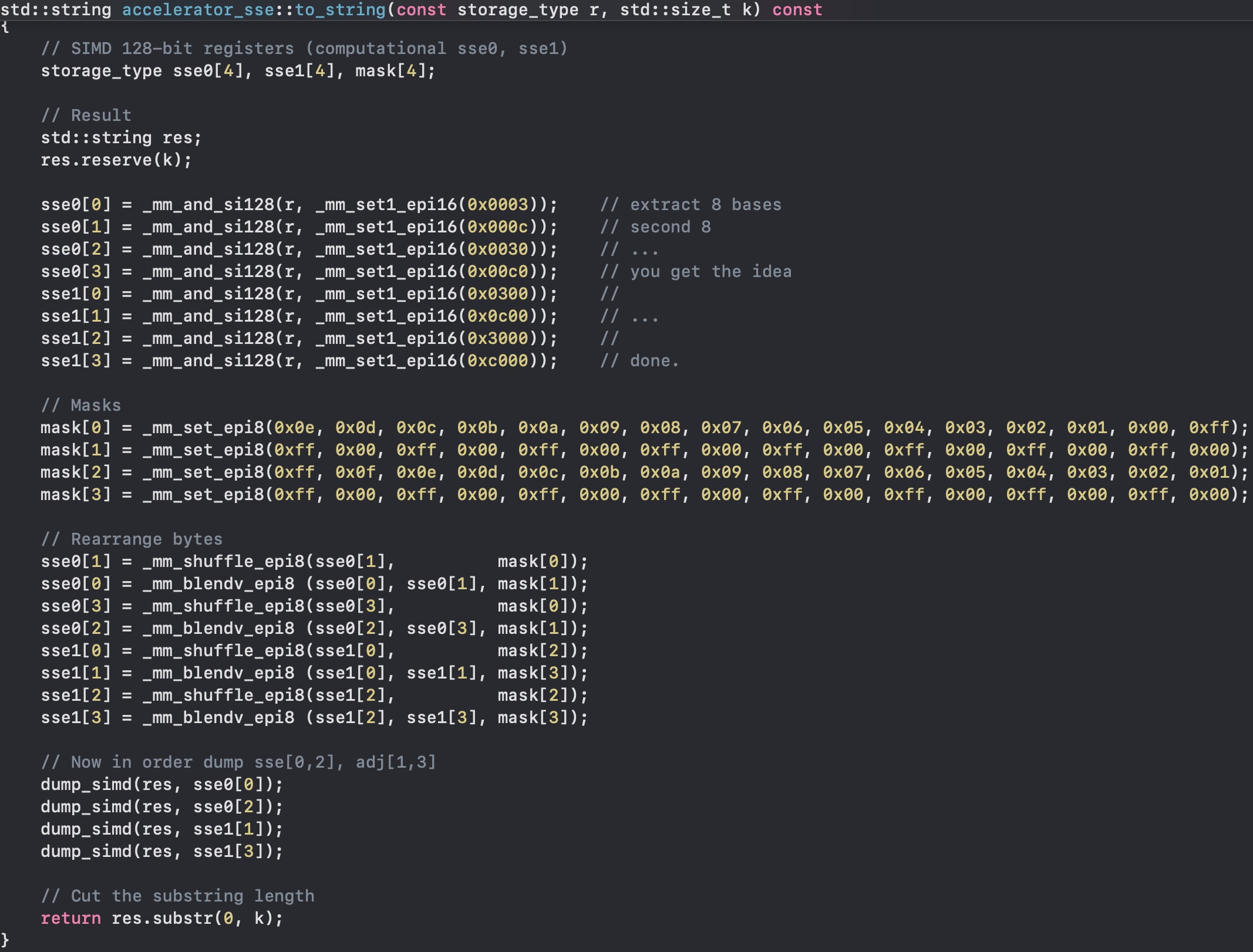
To String
Now we need to test it... so we need a routine to get back a string from a SIMD k-mer. And it is not easy as before.
First, we need to extract the right bases, so we need 8 _mm_and_si128 with the right bitmask, then comes the not-that-simple part. First, we shuffle the bits in the correct order with _mm_shuffle_epi8, and then with _mm_blendv_epi8 we blend the resulting bytes, as we have some bytes in one variable, and others in another one. Finally we can call an auxiliary routine, dump_simd that will append the nucleotides. This conversion to a string does not need to be fast, it is used to test my code, mainly.
Dumping Strings
void dump_simd(std::string &substring, storage_type r)
{
for (int j = 0; j < sizeof(storage_type); j++)
{
unsigned char c = *((unsigned char*)(&r) + j);
switch (c)
{
case 0x00:
substring += 'A';
break;
case 0x0c: case 0x03:
case 0xc0: case 0x30:
substring += 'T';
break;
case 0x02: case 0x08:
case 0x20: case 0x80:
substring += 'C';
break;
case 0x04: case 0x01:
case 0x40: case 0x10:
substring += 'G';
break;
default:
substring += '.';
throw std::domain_error("Unkown character in SIMD register."); // Never happens
}
}
};
Final Words
This was fun, speeding up computations with Intel SSE. The approach is easily expandable to AVX/AVX-2 (256 bits) by doing twice the work, and to AVX-512. It is also quite easy to find the corresponding intrinsics for ARM NEON.
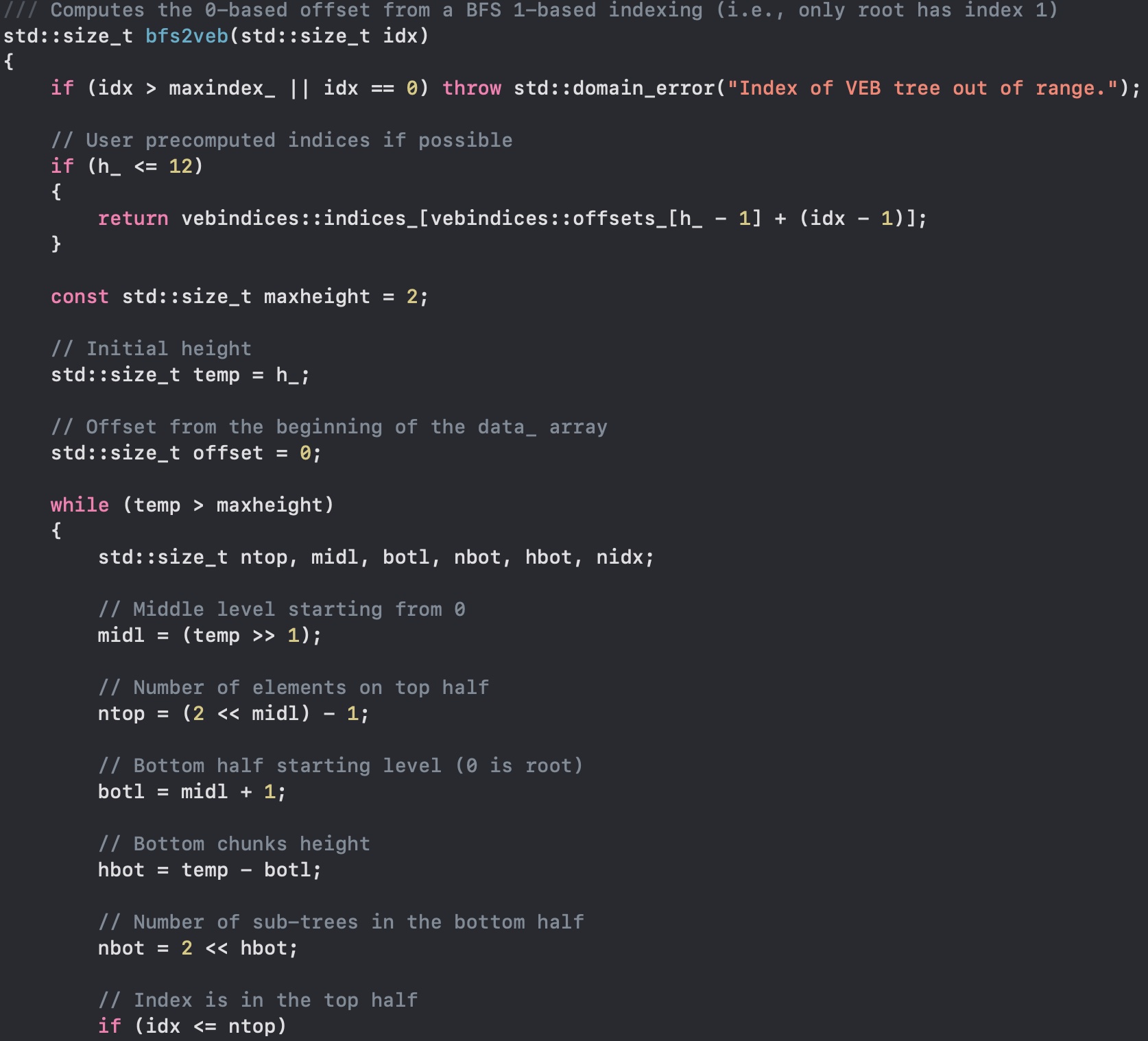
Another fun test was using the Van Emde-Boas cache-oblivious tree, as you can see in the picture. Here I am using the common 1-based complete binary tree numbering (breadth-first), and converting to the VEB memory layout.
But Intel SSE was definitely more fun!